Miracle Math

The Inevitability of Coincidence

Both Sides Brigade

recently contributed a short addition to the Substack/miracle discussion regarding a very unusual event that occurred to him. The TLDR is that he met another young couple with a kid while at the park and discovered that:

1. The couple looked similar to him and his wife

2. Their daughters looked similar

3. Their daughters shared the exact same birth date and hospital

4. The other couple were both wearing crosses

He mused:

… The details seem expertly tuned to push me towards one particular interpretation: That God was showing me a vision of a happy family just like my own, but with the mother and father having faith in Jesus.

Now, rest assured, Both Sides Brigade has not become an evangelist. Rather, he uses this story as an example of how easy it would be for a religiously minded person to see divine providence in coincidences like this. He goes on to question how unlikely such a chance meeting actually is, realize that his overall impression of the event could have been wildly different depending on his predisposition, and ultimately conclude:

In other words, while it originally felt like this crazy coincidence was fine-tuned to address my stubborn lack of faith, I quickly realized there were actually a bunch of different circumstances I could be in where the same general set of details would have tripped a “miracle” alert as well; what felt like a message that was tailor-made for me pretty quickly turned into a general template for projecting a whole range of possible anxieties.

So, in the end his story becomes a parable to teach us about the dangers of reading too much into mere coincidence. A nice lesson.

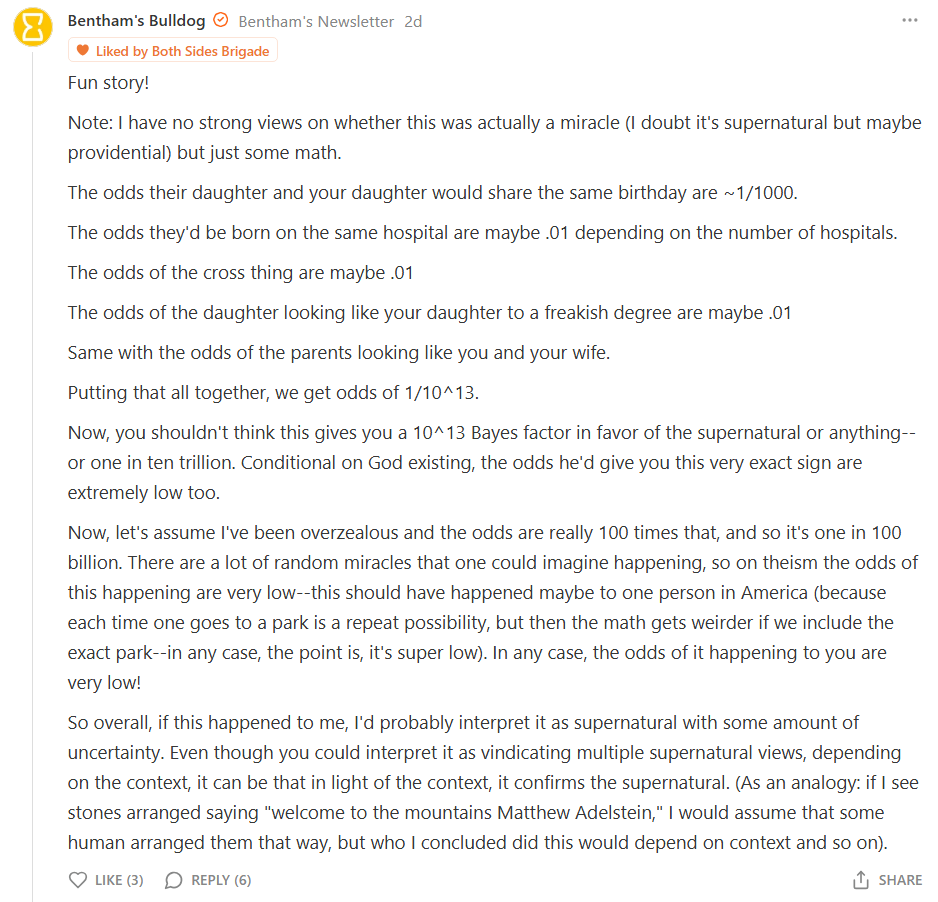
But not everyone agrees with the lesson. Where we will focus in this article is his comments section- specifically, some miracle math by

Bentham's Bulldog

. As is often the case with intelligent people, religion and politics is where emotions get heated and logic goes to die.¹

In the comments he replies with estimates of what probabilities he would assign each particular coincidence. He concludes that the probability of this event occurring is somewhere on the order of 1/10^13 and so “if it happened to him, he would probably interpret it as supernatural with some amount of uncertainty.”

This is the opposite of what one should take away from Both Sides Brigade’s story. So, let’s defend the original message while we review the errors that Bentham is making:

1. Texas Sharpshooter Fallacy

2. Look-Elsewhere Effect

3. Unjustified Assumptions

4. Updating Bayes factor without P(Data|God)

1. Texas Sharpshooter Fallacy

The Texas Sharpshooter Fallacy gets its name from a joke: a cowboy fires wildly at the side of a barn, then walks up afterward and paints a bullseye around the tightest cluster. To anyone passing by, he looks like an expert marksman. However, the truth is that this is a fallacy of retroactively making the hypothesis after first observing the data.²

Here’s a simple example. Imagine shuffling a standard deck of 52 cards and laying them out in a line. When you look over the sequence, you notice that the first four cards are all hearts. You calculate the probability of drawing four hearts in a row to be 13/52 * 12/51 * 11/50 * 10/49 = 0.26%. Wow, that’s about 1 in 400!? Surely that means something strange has happened! But we didn’t predict “the first 4 cards will be hearts” before shuffling- in fact we didn’t predict anything. We are merely drawing a bullseye around anything intriguing that appears; if those first 4 cards had been spades instead, or perhaps the last 4 cards were hearts, we would be equally as surprised- and still calculate the probability the same way.

This is exactly how personal miracles arise. Nobody predicts the details of the miracle in advance- instead, there’s a chance encounter and only afterward do we start connecting the dots.

Tom Hitchner

puts it well with this comment:

What if, instead of the friend having the same birthday as the daughter, the two dads had the same birthday? Or what if the two couples had the same anniversary? Or what if the two dads had been studying abroad in Germany at the same time and had been at the same U2 concert? The number of highly unlikely events that would strike one as meaningful is basically endless, so the absolute probability of any one of them happening is not nearly as important as defining what we will consider miraculous *in advance.* If you rolled a trillion-sided die, getting a result of 1,926,877 would only be remarkable if you predicted that number in advance!

“You know, the most amazing thing happened to me tonight... I saw a car with the license plate ARW 357. Can you imagine? Of all the millions of license plates in the state, what was the chance that I would see that particular one tonight?” —Richard Feynman

In computing all of these probabilities, Bentham is asking: what are the odds of this exact combination? But that’s like walking up to the bullseye after the cowboy finishes painting it, and marveling at his accuracy. It’s like computing the probability of the first 4 cards being hearts. It’s entirely the wrong question to ask, because there was no hypothesis for this exact combination to occur! The right question is: what are the odds of any comparably weird coincidence happening? This effectively erases the bullseye and lets us judge the overall cluster on its own merit. It’s only when we fallaciously draw bullseyes around the coincidences after the fact that it starts to look so surprising.

2. Look-Elsewhere Effect

The look-elsewhere effect is named for the tendency of experimenters, upon initially failing to find interesting results, to ‘look elsewhere’ by running more trials or conducting different tests.³ This is a problem because if you maintain the same criteria for what constitutes ‘interesting’ while dramatically expanding the search space, you are bound to eventually find something statistically significant.

Here’s a quick explainer out of CERN regarding the significance of the effect in physics experiments:⁴

A dangerous beast is hiding in today’s searches for the rare signs of new physics — or even “old” physics, such as the Higgs boson — at the Large Hadron Collider. It is called “Look-Elsewhere Effect”, LEE for insiders. What is it, and why should you care?

Imagine you look for a heavy particle decaying into a pair of hadronic jets: a commonplace test case in high-energy physics. You have your background model, which predicts the observable shape of the di-jet mass distribution, and you know what kind of a bump a new particle signal would produce in that shape. So you search for such a bump in the data, but — not knowing where it might appear — you search everywhere. You have worked all day, and the night is nearing; you prepare yourself a martini and spin your analysis program. To your amazement, the program finds a significant bump at some particular mass value: is it a real signal? To claim it is a new signal, the effect must reach or exceed the “five-sigma” significance level, five standard deviations away from the expectation: that’s a rather silly but well-established rule. But if yours gives only 3.5 or four sigma, are you allowed to get excited and wake up your boss, or should you sit back and sip your martini, with an “I know better” grin on your face?

I claim the latter is a better option. You have fallen prey to the LEE: you looked in many places for a possible signal, and found a significant effect somewhere; the likelihood of finding something in the entire region you probed is greater than it would be if you had stated beforehand where the signal would be, because of the “probability boost” of looking in many places.

Here’s a perhaps more relatable example from out in the real world of miracle hunting: in the 1990s, a group of researchers claimed to have discovered hidden prophecies in the Hebrew Bible. By skipping letters at fixed intervals- a technique called equidistant letter sequencing- they said they could spell out names, events, assassinations, wars, and future leaders. To a casual reader, the odds of finding “Kennedy” encoded in sacred text looked astronomically small. Surely that meant divine authorship?⁵

But what the researchers were doing in their search to ‘break the code’ amounted to trying countless different algorithms to match the data and generate the desired result. Skeptics quickly showed that following this process with Moby-Dick, War and Peace, or indeed any large block of text, would generate very similar ‘miracles.’

To quote the Wiki on this:⁶

This is tantamount in effect to, upon dealing oneself an uninteresting poker hand, continuing to do so in whatever great quantities necessary until one obtains a straight flush, royal flush, or even many such events in sequence, and calling the deck inspired for enabling such a result.

Search long enough, with enough patterns and enough flexibility, and you’ll inevitably uncover eerie coincidences. The Bible Code wasn’t evidence of prophecy- it was merely the look-elsewhere effect in action. When the world is vast and the search rules are open-ended, patterns that feel impossible by chance become not just possible but guaranteed!⁷

Now we go to

Plasma Bloggin'

for another great take:

But even supposing that there was a 1/10^13 chance of all these specific factors lining up, the probability that some other set of factors would line up that feel just as significant is way higher than 1/10^13. And… the probability of something like that happening at some point in his entire life is higher still.

… if you don’t [already] believe in miracles, stuff like this would be really terrible evidence, because the expectation for how often stuff like this should happen, conditional on real miracles never happening, is still, “It should happen very often.”

The lesson here is straightforward: the appearance of improbability alone does not constitute a miracle. With near-infinite ways to slice, shuffle, and reinterpret information, ‘miracles’ like this will emerge constantly. But what feels miraculous is just the statistical inevitability of looking hard and long enough across a completely undefined search space. The real miracle would be finding no coincidences at all.

3. Unjustified Assumptions

The supposed 1 in 10^13 miracle math starts by multiplying five odds together:

• 1/1000 for the same birthdate

• 1/100 for the same hospital

• 1/100 for wearing crosses

• 1/100 for parents resembling each other

• 1/100 for children resembling each other

First of all, this is actually 1/10^11, not 1/10^13. But, lest

Nicholas Halden

appears in my comment section to call me a non-autistic literalist, I will be the first to say this isn’t an important detail. The more important fact is that these are not all independent events! If the parents resemble each other, the children are also more likely to resemble each other. And since they are meeting at this local park, there’s pretty decent odds they were born at the same hospital nearby, etc.

Also, 1% chance of crosses being worn sounds kind of silly considering 60% of American adults are Christian. And the odds of the parents looking similar are probably quite a bit higher than 1%, given ‘similar’ is totally subjective and we are all quite good at finding subjective patterns in random noise. This of course also impacts the probability of the children looking similar.

In this manner, I could easily come up with my own back of the envelope probability assessment of something like 1 in 10 million rather than 1 in 10 trillion. The false precision of even doing the math correctly doesn’t exactly inspire confidence! And if the odds of this specific occurrence are actually closer to 1 in 10 million, suddenly it makes a lot more sense how in combination with the prior fallacies we might expect to see such coincidences all the time.

4. Bayes Factor Updates

Regardless of whether the correct odds are 1 in 10 million or 1 in 10 trillion, the mere surprise itself does not even constitute evidence for the supernatural. All our attention so far has been on how to correctly calculate P(Data|Chance), but to update your prior belief in favor of the supernatural requires you to argue that this exact coincidence was more likely under God than under chance. That is to say, your Bayes factor update depends on both the P(Data|Chance) and the P(Data|God).

To Bentham’s credit, he is of course aware of this, and indeed addresses it at the end of the comment:

Now, you shouldn’t think this gives you a 10^13 Bayes factor in favor of the supernatural or anything… Conditional on God existing, the odds he’d give you this very exact sign are extremely low too.

But then… that’s it. We just jump from there to the implied “well, surely it’s more likely if we allow for the supernatural to exist.” But if you have no model of divine behavior, the answer for P(Data|God) isn’t just “still low but not quite as low”, it’s completely undefined. What’s the probability that God would arrange for you to meet a doppelganger family with a shared birthday in a park? Would God give that exact sign? Why that family, that park, that day, those particular details? Without specifying a distribution of what God tends to do, we can’t assign a probability. And if everything is equally likely under God, then nothing in particular is evidence.

This “miracle math” isn’t just weakened by fuzzy probabilities and independence assumptions- it fails entirely. Without a predictive model of divine action, you can’t compute P(Data∣God). And without that, the Bayes factor collapses into nothing more than a rhetorical gesture.

Conclusion

Imagine a rogue cowboy that fires dozens of shots at the side of a barn.

If he paints a bullseye around the tightest single cluster of holes to make himself look more accurate, that’s the Texas Sharpshooter Problem. He never defined his target (hypothesis) before firing (observing the data).

Now imagine instead that he just left without painting any bullseye, and the next day a committee of townsfolk comes to examine the shots. They wander around looking for any pattern that looks interesting. Eventually, someone notices that one cluster vaguely spells “Hi,” and they circle it with delight. The mistake here is that they aren’t acknowledging how vast the search space is. They are treating that one cluster as if it were a single, isolated experiment, instead of recognizing that dozens of clusters were available to choose from.

Finally, let’s return to our imagined scenario where the cowboy draws the bullseye himself and then leaves. The committee shows up the next day to investigate. They marvel at the perceived accuracy and do some probability calculations to determine there is only a 1/million chance that anyone could be that accurate. Therefore, they decide the shooter was divine. But this is a logical leap that presents no argument for why divinity would make such a result more likely. Rather, because they can’t explain the occurrence, they simply default to attributing it to their prior beliefs.

This is the sleight of hand behind miracle math: to confuse surprise for evidence, and inevitability for design. The only thing improbable coincidences demonstrate is our own talent for painting bullseyes after the shots were already fired.

1. Obligatory

Ethan Muse

comment: “I’m much more confident in the existence of God than dinosaurs!”

2. The Texas sharpshooter fallacy

3. The Look-elsewhere Effect, explained.

4. Should you get excited by your data? Let the Look-Elsewhere Effect decide

5. Best-selling “Bible Code”

6. Look-elsewhere effect

7. Solving the Bible Code Puzzle